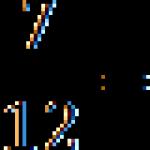Altın bölüm yöntemini kullanarak bir fonksiyonun minimumunu bulun c. Altın oran yöntemine bir örnek

Bu yöntemin ana fikri sayıyı azaltmaktır. n w her adımda (ilki hariç) 1'e (mümkün olan minimum değer) kadar fonksiyon hesaplamaları, ayrıca her adımın yeni güven aralığı içine düşen ikinci deneme noktasının minimumunu ararken kullanılır. Güven aralığının önemli ölçüde iki kattan daha az azalmasına rağmen (ikiliğin aksine), bu yöntem, azalma nedeniyle n w genellikle çok daha hızlı çalışır.

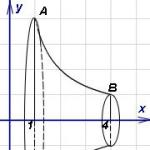
altın Oran segment [ bir, b] böyle bir ara nokta ile bölünmesi olarak adlandırılır İle, hangi ilişkide (Şekil 10.12a) , burada ξ altın orandır.

Şekil 10.12. Segmentin doğrudan ve ters altın bölümleri

x ve segment üzerinden ifade edelim ab segmentler as Ve cb: ac = X ab; cb= X ac= x2 ab.

koşuldan ac + cb = ab bu ifadeleri değiştirdikten ve şuna indirgedikten sonra ab x için aşağıdaki ikinci dereceden denklemi elde ederiz:

x 2 + x - 1 = 0 .

Çözerek kökleri buluyoruz:

Negatif kökü atarak, oranın istenen değerini elde ederiz:

Segmenti böl [ bir, b] yalnızca ileri yönde değil, aynı zamanda ters yönde de mümkündür - Bİle A. benzer nokta D simetrik olarak uzanır İle aralığın orta noktasına göre ( a+b)/2 (Şekil 10.12 b).

oranın değeri ad/ab x'i 1'den çıkararak elde ederiz:

puan D, İle Altın bölümdeki bir segmentin ters ve doğrudan bölünmesini tanımlayan , aşağıdaki özelliklere sahiptir.

1. Segmentin bir kısmını atarsak [ bir,d], O İle d, b].

2. Segmentin bir kısmını atarsak [ c, b], O D kalan kısmın altın oranı [ AC].

Bu özellikler, değerlerin doğrudan ikame edilmesiyle kanıtlanabilir.

Doğrulukla gerekli olduğunu varsayalım e tek modlu bir fonksiyonun minimumunu bulun F(X) Açık [ bir, b].

Ön işlemler ( Adım 0) .

Güven segmenti verilene eşit alınır: A 0 = bir, b 0 = b.

Adımlar Ben(i>0), koşul ( b ben - bir ben > e).

Aşama 1 . 1. İki deneme noktasının konumunun hesaplanması:

X 2 = bir 0 + X( B 0 - A 0)» A 0 + 0,618 (B 0 - A 0);

X 1 = (b 0 + bir 0) -X 2 » A 0 + 0,382(B 0 - A 0).

2. Fonksiyon değerlerinin hesaplanması F(X 1) ve F(X 2).

3. Noktalardaki fonksiyon değerlerinin analizi x 1, x 2 ve ikiliğe benzeterek güven segmentini değiştirmek:

a) de F(X 1) ³ F(X 2) kabul et: A 1 = x 1 , X 1 = x 2 ,B 1 = b 0 ,

b) ne zaman F(X 1) < F (X 2) kabul et: A 1 = bir 0 , X 2 = x 1 ,B 1 = x 2 .

4. Döngü sonunun kontrol edilmesi: if ( B 1 - A 1) > e - döngü devamı, aksi takdirde çıkış.

Adımlar i (i>1) . Önceki yinelemeden ( Ben-1) fonksiyonun bir değeri biliniyor F(X) bir iç noktada X güven segmenti [ bir ben - 1 ; x ben - 1]. Bu nedenle indirgeme için sadece bir yeni deneme noktasının getirilmesi yeterlidir.

1. Yeni bir deneme noktasının konumunun hesaplanması: x¢ =(b ben - 1 + ve ben - 1) - X, fonksiyon değeri hesaplaması F(x¢).

2. Deneme noktaları sipariş etme X, x¢ ve içlerindeki fonksiyon değerleri:

Eğer ( X< х¢ ), O ( X 1 = x; F(X 1)=F(X); X 2 = x¢; F(X 2)=F(x¢) };

aksi takdirde ( X 1 = x¢;F(X 1)=F(x¢) ; X 2 = x; F(X 2)=F(X) }.

Adım 3 ve 4, adım 1 ile aynıdır.

Yöntemin yakınsama oranı ve doğruluğu. Her adımda güven aralığının uzunluğu t = 1/x » 1.618 kez, ardından uzunluk[ A 1 ,B 1 ] uzunluk [ ile ilgilidir bir, b] Aşağıdaki şekilde: B 1 - A 1 = X ( B 0 - A 0) = x ( b-a).

Keyfi bir adım için benzetme yoluyla k güven segmenti uzunluğu: b k - bir k = X k (b-a).

Eşitsizlik oluştuğunda süreç sona erer. b k - bir k = x k(b-a) e.

Buradan adım numarasının k, gerekli doğruluğun elde edildiği e, eşittir k(e)= ]log t ( b-a)/e [ = ]log t M[.

İlk adımda, amaç fonksiyonunun iki hesaplaması yapılır; n w = 1. Bu nedenle, gerekli hesaplamaların toplam sayısı F(X)

P(e)=1 + n wk(e) = 1+] günlük t (( b-a)/e)[ .

Bağımlılık e ( P) eşitlikten buluruz ( b-a)/e = t ( n-1) : e ( P) = (b-a)x (n-1) .

Bağımlılıkların asimptotik büyüme oranları e( N) Ve N(e) altın oran yöntemi için:

e( N) = Ö[( b-a)xn];

P( e) = O=O.

Bu yöntem, formülde olduğu için ikilemden bile daha hızlıdır. P(e) logaritmanın tabanı t » 1.618< 2. Как и дихотомия, он является регулярным. Также он принадлежит к группе так называемых симметричных методов.

Ekstremumu belirlemek için sıralı yöntem denir simetrik , eğer her birinde Ben– güven aralığında bir uç noktası arama adımı [ bir ben, b ben] bir deneme noktası zaten biliniyor X 1 ve amaç fonksiyon değeri F(X 1) içinde. İkinci (yeni) deneme noktası X 2 simetrik olarak tanımlandı X 1 orta noktaya göre ( bir ben + b ben)/2 güven aralıkları: X 2 = bir ben + b ben - X 1 .

Dikotomi yöntemi simetrik değildir.

1. açıklama Bilinen deneme noktası X Simetrik yöntemde 1, değerinden küçük veya büyük olabilir ( bir ben + b ben)/2 .

2. açıklama. Yöntemin simetri özelliği, yeni test noktalarının hesaplanmasını önemli ölçüde basitleştirmeyi mümkün kılar. formül X 2 = bir ben + b ben - X 1, ikinci deneme noktasını hesaplamanıza izin verir x2 ilk nokta nasıl olursa olsun X 1, güven segmentinin orta noktasına göre yerleştirilmiştir (öncesi veya sonrası).

3. açıklama. Çok sayıda yineleme içeren pratik hesaplamalarda, hesaplama hatalarının birikmesi nedeniyle, test noktasının konumu X segmentlerde 1 [ bir ben, b ben] altın orandan önemli ölçüde sapabilir. Bu durumda, sırasıyla, amaç fonksiyonunun gerekli hesaplamalarının toplam sayısı P(e) artacaktır. Bu fenomeni önlemek için, noktanın konumu X fonksiyonun bilinen bir değeri ile formüller tarafından periyodik olarak rafine edilebilir x=bir+ X( b-a)veya x=bir+(1x)( b-a) bu değerlerden hangisine daha yakın olduğuna bağlı olarak.

örnek 1. Bir fonksiyonun minimumunu bulun F(X) =X 2 – 2X Belirli bir doğruluk e = 0.5 ile altın bölüm yöntemine göre güven aralığında.

Çözüm.

Adım 0. A 0 = bir, b 0 = b.

Aşama 1. İki deneme noktasının konumunun hesaplanması: X 2 = bir 0 + X( B 0 – 0) "1,3124; X 1 = (B 0 +a 0)-X 2) » 0,8876. İçlerindeki işlev değerleri: F(x 1) = -0,9874; F(X 2) = -0,7768. Çünkü F(x 1)<F(X X 2 ;B 0 ].Yeni bir güven segmenti [ A 1 ;B 1 ] = .

B 1 -A 1 = 1,1124 > e = 0,5; aramaya devam edin.

Adım 2. Güven çizgisi sınırları A 1 = 0,2; B 1 = 1,3124. Fonksiyonun o noktadaki değerini bilir. X" 0,8876,F(X) = -0,9874.

Yeni deneme noktası: x¢ =(B 1 +a 1) - 0,8876 » 0,6248. Yeni noktada fonksiyon değeri x¢: F(x¢) = -0,8592.

Çünkü x¢<х, o zaman kabul ediyoruz X 1 = x¢;F(X 1) =F(x¢); X 2 = x; F(X 2)= F(X).

Çünkü F(X 1) >F(X 2), ardından güven segmentinin bir kısmını atıyoruz [ A 1 ;X 1 ].Yeni bir segment [ A 2 ; b2 ] = .

B 2 -A 2 \u003d 0.6878\u003e e \u003d 0.5; aramaya devam ediyoruz.

Aşama 3. A 2 = 0,6246; B 2 = 1.3124. Noktadaki fonksiyonun değeri biliniyor X" 0,8876, F(X) = -0,9874.

Yeni deneme noktası: x¢ =(B 2 +a 2) - 0.8876 » 1.0494 .. Fonksiyonun yeni noktadaki değeri x¢: F(x¢)= --0,9976.

Çünkü x¢>x, o zaman kabul ediyoruz X 1 = x; F(X 1) =F(X); X 2 =x¢; F(X 2)= F(x¢).

Çünkü F(X 1)>F(X 2), ardından güven segmentinin bir kısmını atıyoruz [ A 1 ; X 1 ] ve segmenti alın [ A 3 ; B 3 ] = .

B 3 -A 3 =0,4248 < e =0,5;следовательно, поиск завершен.

Cevap. 3 adım tamamlandı, 4 test noktası kullanıldı. Bulunan nihai güven aralığı: [ A 3 ,B 3] = uzunluk 0,4248.

Örnek 1 p.10.3'ten görülebileceği gibi, dikotomi yöntemine göre gerekli fonksiyon hesaplamalarının sayısı 6'dan 4'e düşürülmüştür.

Bilgiyi test etmek için sorular.

1. a) Segmentin altın kesitine, b) segmentin doğrudan ve ters altın kesitine ne denir?

3. Güven segmentini azaltırken altın bölümün hangi özelliği kullanılır?

4. Hangi yöntemlere simetrik denir ve örnek noktaların hesaplanmasını basitleştirmek için simetri nasıl kullanılır?

5. Altın oran yönteminde ilk ve sonraki adımlar nasıl gerçekleştirilir?

6. Altın oran yöntemi neden dikotomiden daha hızlıdır?

Altın Oran Yöntemi Hakkında:

Kesinlikle basit ve hızlı bir yöntem. Ve her zaman olduğu gibi, hız isabetliliğe katkıda bulunmaz. Bu, belirli bir arama aralığında birkaç minimum (maksimum) varsa, bu algoritmanın kolayca yerel (en büyük değil, mutlak değil) bir ekstremum döndürebileceğini söylüyorum.

Egzersiz yapmak:

Extremum arama algoritmasını test etmenizi sağlayan bir program yazınız. altın oran yöntemi beş keyfi fonksiyon örneğinde. Arama için ilk veriler, aralığın sınırları, doğruluğu ve ekstremum tipi (MAKS veya MİN) olmalıdır. program göstermelidir belirli bir aralıkta bir fonksiyonun grafiği ve uç noktanın koordinatları.

Programı yayınlamak mantıklı aşağıdaki sınıflar ve modüller:

Form üzerinde olduğu gibi test süreci için gerekli kontrollerin yer alacağı Excel sayfa modülü (SheetGoldCutting);
Veri giriş formu FormDann;
Belirli bir doğrulukla bir uç noktanın koordinatlarını hesaplayan ExtremGC sınıfı ve ayrıca belirli bir aralıkta fonksiyon grafiğinin bir nokta dizisini (şema üzerinde görüntülemek için);
Global sabitleri, değişkenleri ve fonksiyonları açıklamak için GoldCutting standart modülü.

Örneğin, yani...

Şek.1 Grafik, iki komut düğmesi ve işlev seçim düğmeleri içeren Excel çalışma sayfası

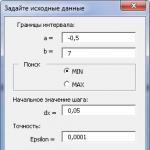
Şekil 2 İlk verileri girmek için form

Bu form, tıklandığında açıkça çağrılır. ilk komut düğmesi(bir Excel sayfasında bulunur) veya dolaylı olarak, tıklandığında ikinci komut düğmesi(bir Excel sayfasında bulunur), ilk veriler algoritmayı başlatmak için gerekli koşulları sağlamaz.
Kullanıcının rahatlığı için tüm unsurlar Metin kutusu girişe izin ver sadece sayısal değerler.
Düğmeye tıklayın "İptal etmek" tüm değişkenler, formun açıldığı sırada var olan değerleri alacaktır.

Bir dosya açıldığında (makrolar etkinleştirilmişse) veya makrolar etkinleştirildiğinde (dosya açıldığında devre dışı bırakılmışlarsa), hazırlanan işlevlerden birini varsayılan test işlevi olarak ayarlamak (tanımlamak) için bir olay işleyici yürütülür. Bunu yapmak için birini işaretlemek yeterlidir (örneğin, ilk) Seçenek tuşu(veya genellikle çağrıldığı şekliyle - bir radyo düğmesi) ve bu düğmeye atanan makroyu çağırın.

Özel Alt Workbook_Open()
"bu kitapta radyo düğmeleri 5'ten 9'a kadar numaralandırılmıştır.
Bu yüzden varsayılan olarak ilk düğmeyi vurgularım.
Sheets(1).Shapes("Seçenek Düğmesi 5").ControlFormat.Value = 1
SheetGoldCutting.OptBut1_Click
son alt

Yöntem Algoritma sınıf EkstremGC, aslında uç noktanın koordinatlarının belirlenmesini gerçekleştiren şuna benzer:

"Bir segmentte bir fonksiyonun uç noktasını bulma. Altın oran yöntemi
Genel Alt Algoritma(v1 Çift Olarak, v2 Çift Olarak, v3 Çift Olarak, v4 Çift Olarak, Maks'ı Boole Olarak Bul)
Dim x1 Çift Olarak, x2 Çift Olarak, y1 Çift Olarak, y2 Çift Olarak, sme Çift Olarak
Bağımsız değişkenin geçerli olup olmadığını kontrol etmek için FullArrayOnly v1, v2, v3, v4"

Kötü DeğilseDannSonra

Zc = (1 + Kare(5)) / 2
n = 0 "bölme sayısı (sınıf modül değişkeni)
b - a > ep iken yapın
küçük = (b - bir) / zc
x1 = b - küçük: x2 = a + küçük
y1 = theFunc(x1): y2 = theFunc(x2)
Eğer findMax O zaman
"maksimum ara
y1 a = x1 ise
Başka
b=x2
Eğer Sonlandır
Başka
"minimumu ara
y1 >= y2 ise O zaman
bir = x1
Başka
b=x2
Eğer Sonlandır
Eğer Sonlandır
n = n + 1 "bölme sayısı (sınıf modül değişkeni)
döngü
dxk = Abs(b - a) " son adım değeri
xe = (a + b) / 2: ye = theFunc(xe) " sonuç: ekstrem nokta koordinatları

eğer biterse
son alt

Nerede
Yalnızca Tam Dizi- bağımsız değişkenin kabul edilebilirliğini kontrol etmek ve grafik noktaları dizisini doldurmak için özel bir sınıf yöntemi;
BadDann– argüman kabul edilebilirlik bayrağı;
zc altın bölüm sabitidir;
bir, b– aralık sınırları;
ep belirtilen arama doğruluğu ε ;
max bul arama modunu karakterize eden bir parametredir (ne zaman doğru maksimumu aramak YANLIŞ- minimum);
theFunc(x Çift Olarak) Çift Olarak bağımsız değişkenin değerine bağlı olarak test edilen işlevin değerini döndüren bir sınıf yöntemidir.

Kodun geri kalanıyla ilgilenenler için lütfen iletişime geçin ...
Gereksinimlerinize uyacak şekilde projede bir şeyi değiştirmeniz gerekirse (örneğin, işlevleri değiştirin) - lütfen, sorun olmayacak!

kaynak kodu zaten açık. Kullanmak !

Veri giriş formunu görmüyorsanız, makroları etkinleştirmeyi unutmuşsunuz demektir...

İlk fonksiyon için argüman değerlerinin sıfırdan küçük veya sıfıra eşit olamayacağına dikkatinizi çekmek isterim.

Algoritmanın nasıl hata yaptığını ve mutlak bir uç nokta yerine yerel bir uç nokta bulduğunu görmek için, açık bir periyodikliğe sahip 4 veya 5 işlev için yeterince büyük bir aralık ayarlayın (örneğin: 0'dan 25'e kadar) ...

altın oran yöntemi

Böyle simetrik bir nokta düzenlemesi düşünün X 1 ve X segmentte 2 [ A; B], bunlardan biri bir test noktası olur ve orijinal segmentin bir kısmının çıkarılmasından sonra yeni bir segment elde edilir. Bu tür noktaların kullanılması, ilki hariç, segment eleme yönteminin her yinelemesinde kendimizi yalnızca bir değer belirlemekle sınırlamamıza izin verir. F(X), önceki iterasyonlardan birinde zaten başka bir değer bulunduğundan.

Önce bir parçayı ele alalım ve kesinlik için, azaldığında bu parçanın sağ tarafının dışarıda kaldığını varsayalım. İzin vermek X 2 = , ardından simetrik olarak yerleştirilmiş bir nokta X 1 \u003d 1- (Şek. 2.2).

Pirinç. 2.2.

deneme noktası X 1 segment deneme noktasına gidecek X 2 = 1- yeni bölüm. işaret etmek X 2 = ve X 2 = 1- Segmentlere bölünmüş ve aynı oranda, eşitlik veya sağlanmalı, buradan pozitif bir değer buluyoruz... Böylece, X 1 = 1- = , .

keyfi bir bölüm için [ A; B] test noktaları için ifadeler şu şekilde olacaktır

1. Noktalar X 1 ve X 2 aşağıdaki özelliğe sahiptir: her biri segmenti böler [ A; B] eşit olmayan iki parçaya bölün, böylece tüm parçanın uzunluğunun daha büyük parçasının uzunluğuna oranı, parçanın daha büyük ve daha küçük parçalarının uzunluklarının oranına eşittir. Bu özelliğe sahip noktalara denir altın oranın püf noktaları segment [ A; B].

2. Deneme noktalarına sahip bölümlerin ortadan kaldırılmasının her yinelemesinde, bunlardan biri bir sonraki bölüme gider ve değer F(X) bu noktada hesaplanmamalıdır. Yeni segment [ A; X 2 ], ardından orijinal segmentin deneme noktası ona geçerek ikinci deneme noktası olur ( X 2 "= x 1) (Şek. 2.2). Segmente geçiş durumunda [ X 1 ; B] orijinal bölümün deneme noktası, bölümün ilk deneme noktası olur [ X 1 ; B].

3. Bunu kontrol etmek kolaydır X 1 =a+b-X 2 , ve X 2 =a+b-X 1 . Bu nedenle, altın oran yönteminin her iterasyonunda, yeni segmentin eksik deneme noktası, kendisine geçen deneme noktasından toplama ve çıkarma kullanılarak bulunabilir.

4. Altın oran yöntemi kullanılarak yapılan hesaplamalar sonucunda yaklaşık değer olarak X* elde edilen segmentlerin sonunun ortasını alabilirsiniz.

Her yinelemede, minimum nokta arama segmenti aynı oranda azalır, dolayısıyla sonuç olarak P yinelemelerde uzunluğu olur. Yani doğruluk N nokta tanımı X* sonrasında P yinelemeler eşitlikten bulunur ve nokta için aramayı sonlandırmanın koşulu X* kesinlik ile n eşitsizliğidir.

Dikotomi ve altın oran yöntemlerini kullanan bir çözüm örneği

d=2, e=1 olan bir fonksiyon verildiğinde

Aralığın minimumunu bulmak gerekir , nerede, yani. segmentte

e \u003d 0.001 doğrulukla yineleme sayısını verecek bir program yazın

İki yöntemle çözün: dikotomi ve altın oran

İkilem çözümü:

f1'den beri

Altın oran yöntemiyle çözüm:

f1'den beri

Dikotomi ve altın oran yöntemlerini uygulayan programın listesi Ek A'da sunulmuştur.

f(x)=(100-)'yi en aza indirmek istediğimiz Örnek 2.6'daki sorunu yeniden ele alalım. X) £60 aralığında 2 adet X 150 sterlin. Birim uzunluk aralığına geçmek için w=( X- 60)/90. Böylece, sorun aşağıdaki formu alır: en aza indirmek için f(w) = (40 – 90w) 2 0£w£1 kısıtlaması altında.

Yineleme 1. ben 1 = (0, 1);L1= 1. Fonksiyon değerlerinin ilk iki hesaplamasını yapalım:

w 1 = t = 0,618, f(w1) = 244,0

w 2 = 1-T= T 2 = 0,382, f(w2) = 31,6

Çünkü f(w2)< f(w 1) Ve w 2< w 1 , aralık w ³ w 1 hariç.

Yineleme 2. ben 2 =(0. 0,618);L2 = 0,618 = T. Fonksiyon değerinin bir sonraki hesaplaması şu noktada gerçekleştirilir:

w 3 \u003d t-t 2 \u003d t (1-t) \u003d t 3\u003d 0,236, f (w 3) \u003d 352.

Çünkü f(w 3) > f (w 2) Ve w 3< w 2 , w £ w 3 aralığı hariç tutulur.

Yineleme 3. ben 3 =(0,236, 0,618); L 3 = 0,382 = t2. Fonksiyon değerinin bir sonraki hesaplaması, aralığın sol sınır noktasından t ´ (elde edilen aralığın uzunluğu) mesafesinde bulunan bir noktada veya (1- T) ´ (aralık uzunluğu) sağ sınır noktasından. Böylece,

w 4 =0,618 – ( 1-t)L 3= 0.618 - 2 L 3 0.618 - t 2 (t 2) = 0.618 - t4 = 0,472, f(w4) = 6,15.

Çünkü f(w4)< f (w 2) Ve w4 > w2, aralık w £ w2 hariç.

Sonuç olarak, aşağıdaki belirsizlik aralığı elde edildi: 0,382 £ w w için 0,618 £ veya 94,4 £ X Değişken için 115,6 £ X.

Arama sırasında altı işlev değeri hesaplaması yapıldıysa, değişken için sonuç aralığının uzunluğu w eşittir

t N -1 = t 5 = 0,09,

değişken için 8.1'lik bir uzunluk aralığına karşılık gelir X. Karşılaştırma için, benzer bir durumda, aralığı ikiye bölme yönteminin 11.25 uzunluğunda bir aralık elde etmeye yol açtığını hatırlıyoruz.

Genel durumda, belirsizlik aralığının sağ ve sol sınır noktaları (bunları XR Ve XL) biliniyorsa, altın oran yöntemine göre elde edilen sonraki tüm test noktalarının koordinatları formüller kullanılarak hesaplanabilir.

w = XR - tn veya w = XL + tn, önceki yinelemede hangi alt aralığın hariç tutulduğuna bağlı olarak - sol veya sağ. Yukarıdaki formüllerde, t n işaretlenmiş N-inci derece T, Nerede P işlev değeri değerlendirmelerinin sayısıdır.

Altın bölüm yöntemini kullanan arama, işlev değerlerinin belirli sayıda hesaplanmasına (ve dolayısıyla belirsizlik aralığının boyutuna) veya istenen işlev değerinin göreli doğruluğuna ulaşıldığında sonlandırılabilir. Her iki kriterin aynı anda kullanılması daha çok tercih edilir.

Aralık eleme yöntemlerinin karşılaştırılması. Aşağıda, aralıkları ortadan kaldırmak için dikkate alınan yöntemlerin göreli verimliliklerini karşılaştırıyoruz. Yavaş hareket eden belirsizlik aralığının uzunluğunu şu şekilde gösterelim: L1 ve elde edilen aralığın uzunluğu N fonksiyon değerlerinin hesaplanması, - aracılığıyla L N. Aralıkları ortadan kaldırmak için şu veya bu yöntemin etkinliğinin bir göstergesi olarak, ilk aralıktaki göreli azalmanın özelliğini dikkate alıyoruz. FR(N)=L N /L 1

Aralığı ikiye bölme yöntemini ve altın bölüm yöntemini kullanırken, ortaya çıkan aralığın uzunluğunun şu olduğunu hatırlayın: L 1 (0,5) N /2 Ve L 1 (0,618) N-1 sırasıyla. Bu nedenle, sonraki aralıktaki göreli azalma N fonksiyon değerlerinin hesaplanması eşittir

FR(N) = (0,5) N /2 aralığı ikiye bölme yöntemi için;

FR(N) = (0,618) N-1 Altın oran yöntemi için.

Karşılaştırma için, fonksiyonun N eşit aralıklı noktalarda değerlendirildiği tek tip arama yöntemini de dikkate alıyoruz (bu durumda, L 1 aralığı (N+1) eşit uzunluk aralıklarına bölünür L 1 /(N+ l)). f(x) fonksiyonunun minimumunun gözlemlendiği nokta x* olsun. O zaman gerçek minimum nokta f(x) aralıkta bulunur.

bu nedenle L N = 2L 1 /(N+l). Bu nedenle, tek tip arama yöntemi için FR(N)=2/(N+1).

Masada. 6.2, üç arama yöntemi için seçilen N'ye karşılık gelen FR(N) değerlerini gösterir. Tablodan, altın oran yöntemini kullanarak aralıktaki göreli azalmanın değerinin arandığını takip eder.

Tablo 6.2

aynı sayıda fonksiyon değeri hesaplaması ile orijinal aralıktaki en büyük göreli düşüşü sağlar. Öte yandan, belirli bir miktarda göreceli aralık azaltma veya belirli bir doğruluk derecesi elde etmek için gereken fonksiyon değeri hesaplamalarının sayısı da karşılaştırılabilir. FR(N) = E değeri verilirse, N değeri aşağıdaki formüller kullanılarak hesaplanır:

Aralık yarıya indirme yöntemi için

N=2ln(E)/ln(0,5),

altın oran yöntemi için

N=1+,

tek tip arama yöntemi için

Masada. 6.3, minimum noktanın koordinatlarını belirli bir doğrulukla belirlemek için gereken fonksiyon değerlerinin hesaplama sayısına ilişkin verileri gösterir. Aynı verili doğruluğu elde etmek için fonksiyon değerinin en az sayıda değerlendirilmesini gerektirdiğinden, altın oran yönteminin diğer iki yöntemden daha verimli olduğu bir kez daha vurgulanmalıdır.

Yöntem, geçerli segmenti [ A,B], istenen ekstremumun bulunduğu yerde, minimum (maksimum) içeren bir sonraki parçayı belirlemek için altın oran kuralına uyarak iki eşit olmayan parçaya bölünür.

Altın oran kural tarafından belirlenir: tüm parçanın daha büyük kısmına oranı, parçanın büyük kısmının küçük olana oranına eşittir. İki noktadan memnun C Ve D, segmentin ortasına simetrik olarak yerleştirilmiştir.

Kıyasla R(C) Ve R(D) maksimumu içeren bir sonraki segmenti belirleyin. Eğer R(D) > R(C), sonra bölüm [ İle,B], Aksi takdirde, segment [ A, D].

Yeni segment yine altın oran kuralına göre eşit olmayan kısımlara bölünür. Unutulmamalıdır ki, nokta D aynı zamanda segmentin altın bölümünün bir noktasıdır [ İle,B], onlar.

Bu nedenle, sonraki her yinelemede (ilk segmentte yöntemin "başlatılması" hariç), optimallik kriterinin yalnızca bir değeri hesaplanmalıdır.

Segmentte maksimum değerin olduğu yeni bir noktayı hesaplamak için analitik formüller vardır. R(X), hangisini elde etmek kolaydır:

Aramanın bitmesinin koşulu, belirtilen hatadan küçük olan maksimumu içeren segmentin değeridir.

Yöntem, çözüme diğer birçok yöntemden daha hızlı yakınsama sağlar ve açıkça yalnızca tek ekstremal fonksiyonlar için uygulanabilir.

Şek. Şekil 3, altın oran yöntemini kullanarak bir fonksiyonun maksimumunu aramanın iki aşamasını göstermektedir.

Pirinç. 3. Altın bölüm yönteminin gösterimi: 1 - ilk aşamadan sonra işlevin istenen maksimum değerini içeren aralık (noktalardaki ilk altın bölüm) C Ve D); 2 – aynı, ikinci aşamadan sonra (yeni nokta e ve eski nokta D)

Fonksiyon Minimizasyonu için Altın Oran Yöntemi Algoritması.

İlk aşama. Belirsizlik aralığının kabul edilebilir bir sonlu uzunluğunu seçin ben> 0. [ A, B] ilk belirsizlik aralığıdır. Koymak
Ve
. Hesaplamak R(C) Ve R(D), k = 1 koyun ve ana aşamaya geçin.

Ana sahne.

Aşama 1. Eğer B k – A k < ben o zaman dur; minimum nokta [ A k , B k]. Aksi takdirde, eğer R(C k) > R(D k), ardından 2. adıma gidin ve eğer R(C k) ≤ R(D k), ardından 3. adıma gidin.

Adım 2 Koymak A k +1 = C k Ve B k +1 = B k ,
. Hesaplamak R(D k+1) ve 4. adıma gidin.

Aşama 3 Koymak A k +1 = A k Ve B k +1 = D k ,
. Hesaplamak R(C k+1) ve 4. adıma gidin.

Adım 4 Yer değiştirmek k Açık k + 1 ve 1. adıma gidin.

Örnek.

Verilen bir işlev R(X) = D günah (Ah B +C), burada katsayılar aşağıdaki değerlere sahiptir: bir = 1,0,B = 1,0, Ç = 1,0, D = 1.0. Aralıktaki maksimum değeri bulun: [-1, 2]. Hata tarafından ayarlanır x: e =0,05.

Hesaplama sonuçları. Yöntemi "başlatmak" için, [-1, 2] kesimi için altın bölümün iki simetrik noktasını bulalım:

X 1 =0,145898, X 2 =0,85410197.

Bu noktalardaki kriterlerin değerleri sırasıyla R(x 1)=0,911080, R(x2) = 0,960136. Bu nedenle, yeni segment, içinde bulunan değerlerin maksimumu olan R. Yeni segment için altın bölüm noktası x 3 \u003d 0,58359214 olacaktır, a R(X 3) =0,99991813. Ayrıca bir sonraki adımda sadece en iyi noktaların koordinatları, adım numarası ve bu noktalardaki kriter değerleri verilmektedir.

X 3 = 0,58359214; R3 = 0.99991813;

X 4=0,58359214; R4 = 0,99991813

X 5 = 0,58359214; R5 = 0.99991813;

X 6 = 0,58359214; R 6 \u003d 0,99991813

X 7 = 0,58359214; R7 = 0.99991813;

X 8 = 0,55920028; R8 = 0.99993277;

X 9 = 0,55920028; R 9 \u003d 0,99993277.

Optimallik kriterinin toplam 10 hesaplaması yapılmıştır.